I’ve now spent a few weekends working on my WDR system. The one overriding thing that gets to me is just how bad the information is out there. There are lots of things that aren’t quite spelled out well enough for non-maths gods like me.
Anyway. On to the basics of the transform. Anyone who has dealt with wavelets knows that you decompose the image into 4 sections.
LL LH
HL HH
You then go on to to the same process to the LL portion of the image. Rinse and repeat this method for as long or as short as you like (You don’t have to even do more than the first decomposition). Effectively what you now have is high pass information and low pass information. The low pass is the LL section. The highpass sections give you the horizontal high pass, the vertical high pass and the diagonal high pass (Effectively edge detect in 3 different directions). These are generated by first applying the wavelet transform horizontally and then applying it on the resulting image vertically. The joy of the wavelet transform is that it is reversible. Exactly so. This means you can re-construct the original image from the various high and low passes losslessly. Its worth bearing in mind that this can be trivially extended into 3 dimensions to compress video. I keep wondering whether you’d be able to re-sample frame rates nicely using this sort of video transform but thats an aside.
Ok so lets get on to a wavelet transform. I’m going to use the Daub5/3 wavelet because it can be done entirely with integers which means there are no rounding issues. It is truly lossless.
The equation is as follows (Taken from: A Low-power, Low-memory System for Wavelet-based Image Compression by Walker, Nguyen & Chen):
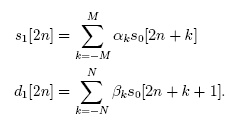
My first thought on seeing that was WTF!? However I carried on reading through the excellent paper linked above.
It turns out that there is a more efficient (And simpler) form of this wavelet transform known as a lifting wavelet transform. The transform looks like the following:
- s0 is the Image we are performing the transform on. It is a very standard image in the 8-bit 0->255 range.
- s1 is the low passed output of the transform.
- d1 is the high passed output of the transform
- The whole n thing is a bit confusing. 2n is every other pixel in the source image. It is not, however, every other pixel in the destination image. The indication of 2 indicates a step of 1 pixel when dealing with s1 and d1. This is massively confusing for the likes of me.
First thing to notice is that the calculation for s1 contains usage of d1. Not just d1 but the previous pixel’s d1.
(At this juncture I’d like to point out that the aforementioned paper gives another equation as an “integer-to-integer” equation. Try as I might I could never get this working. The equation I’ve just posted works perfectly).
I’m going to move on to some code now.
const int n = (x) + (y * pixelPitch);
const int n2 = (x / 2) + (y * pixelPitch);
const int s = n2;
const int d = n2 + widthDiv2;
const int16_t d1 = pixelsIn[n + 1] –
(((pixelsIn[n] + pixelsIn[n + 2]) >> 1));
const int16_t s1 = pixelsIn[n] +
(((pixelsOut[d – 1] + d1) >> 2));
pixelsOut[d] = d1;
pixelsOut[s] = s1;
The above is a simple code version of the wavelet transform. There is a problem with it, however. You’ll note that due to the fact it uses the previous high pass pixel outputed in the s1 calculation and the next pixel from the input in the d1 calculation.
This means that we get a break down at either end of a line. Fortunately this is fairly easy to rectify (Though I can find no mention of it anywhere). For the first pixel on a line you can just use d1 twice. For the last pixel you use the current pixel twice. Its an easy solution and works well.
When doing a vertical decomposition the equation is much the same but instead of doing -1, +1 and +2 by adding/subtracing the pixel pitch (The width of the entire original texture) instead of 1. Doing this twice over performs the appropriate 2D forward wavelet transform.
Inverting the wavelet transform is pretty simple as well. You can easily get the reverse of the transform by re-arranging the equations. Bear in mind, however, that you need to step from the right hand side of the image towards the left (ie backwards) to re-construct the image. The trick above for handling the special cases at either end of the line works just as well for the inverse transform.
The code for the central part of the inverse transform will look something like this:
const int n = (x) + (y * pixelPitch);
const int n2 = (x / 2) + (y * pixelPitch);
const int s = n2;
const int d = n2 + widthDiv2;
const int16_t s0 = pixelsIn[s] –
(((pixelsIn[d – 1] + pixelsIn[d]) >> 2));
const int16_t s1 = pixelsIn[d] +
(((s0 + pixelsOut[n + 2]) >> 1));
pixelsOut[n] = s0;
pixelsOut[n + 1] = s1;
Anyway I hope thats slightly useful. It certainly will be to me when I inevitably forget what I’ve done 🙂
Tags: wavelets